[논문 리뷰] Predictive Coding (1) | A tutorial on the free-energy framework for modelling perception and learning, Rafal Bogacz
paper url : https://www.sciencedirect.com/science/article/pii/S0022249615000759
이 논문은 Predictive Coding의 주요 이론인 "free-energy framework"에 대해 접근할 수 있도록 간단한 상황부터 차근차근 설명해가는 튜토리얼 논문입니다. 즉, 본래 논문인 "The free-energy principle: a unified brain theory?, Karl Friston"보다 쉽게 해당 내용을 설명하는 것이 목적이라 할 수 있습니다. 하지만 그러다보니 신경과학적 또는 행동학적 근거 등 디테일한 부분은 논문에 포함되어 있지 않으니 이에 대한 것은 다른 자료를 찾아봐야 합니다.
사람은 감각기관에서 정보를 "측정"하고 그것을 통해 여러 특징을 "추출"합니다. 하지만 이것에는 항상 오차가 존재하기 마련입니다. 이 오차를 수정하는 작업을 거치는 과정이 바로 Predictive Coding입니다. 다시 말해서 측정한 정보에서 본래 특징을 예상하여 추출하는 것입니다. 예를 들어 받은 빛의 양으로부터 물체의 크기를 예상하는 것이 그 예시라고 할 수 있습니다. 이 Predictive Coding은 앞의 예시와 같이 실제로 Visual Information을 처리하는 것에 대해 주로 발달해 왔습니다.
이 논문에서는 가장 간단한 상황(측정 값과 추출값이 서로 독립적인 하나의 변수임)을 먼저 설계하고 이를 여러개의 변수로 확장합니다. 우선 용어 정의를 보면 v가 추출하려는 자연에서의 특징, u가 측정된 값에 해당되며 v라는 특징이 만들어내는 측정값 u의 평균은 g(v)라는 수식으로 나타내집니다. 또 아래 수식들과 같이 p(u|v)와 p(v)의 오차는 정규분포를 통해 표현됩니다.


우리가 구해야 하는 것은 측정값이 u일때 어떤 v가 실제 v일지 예측하는 것입니다. 따라서 우리가 구해야 하는 것은 u가 주어졌을때 p(v|u)가 극값이 되게 하는 v를 구해야 하는 것입니다. 우리는 이것을 phi로 표현할 것이고 Bayes' theorm을 사용하면 p(v|u) = p(u|v)p(v) / p(u)로 표현이 가능합니다. 여기에서 phi의 극값고 p(u)항은 무관하기 때문에 이것이 최대가 되게 하는 phi는 아래 F가 최대가 될때와 동일합니다.

또 이것을 미분한 값은 아래와 같습니다. 하지만 우리의 목적은 단순히 미분 값을 구하는 것이 아닙니다. 우리의 목적은 이 최적화 과정을 가능하게 하는 "신경 회로"를 구하는 것에 있습니다. 이러한 이유 때문에 이를 단순히 계산하는 것이 아니라 아래 변수들로 치환하는 과정을 거칩니다.
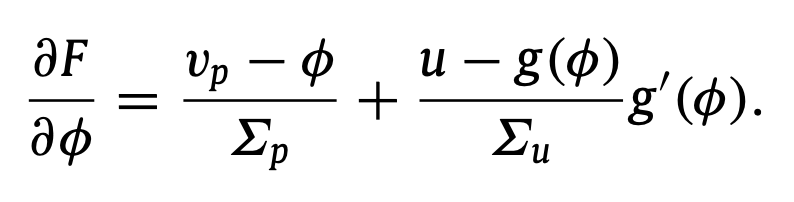

이들 각각에 대해 평형이 되게 만드는 미분 값을 정리하면 아래와 같게 되기도 합니다. 실제로 각 feedback 되는 값이 0이 될때 즉 평형상태를 생각해보면 위 식들이 등호가 성립할 때가 나오게 됩니다.


여기서 마지막으로 g(v, theta) = theta *h(v)라고 나타내면 놀랍게도 이렇게 만든 수식을 Hebbian Learning과 Local Plasticity로 표현하는 것이 가능합니다. 정말 간단한 계산만 해보면 위 수식대로 feedback이 진행된다는 사실과 중간에 있는 가중치가 presynaptic과 postsynaptic frequency에 의해 hebbian learning 된다는 사실을 알 수 있습니다.
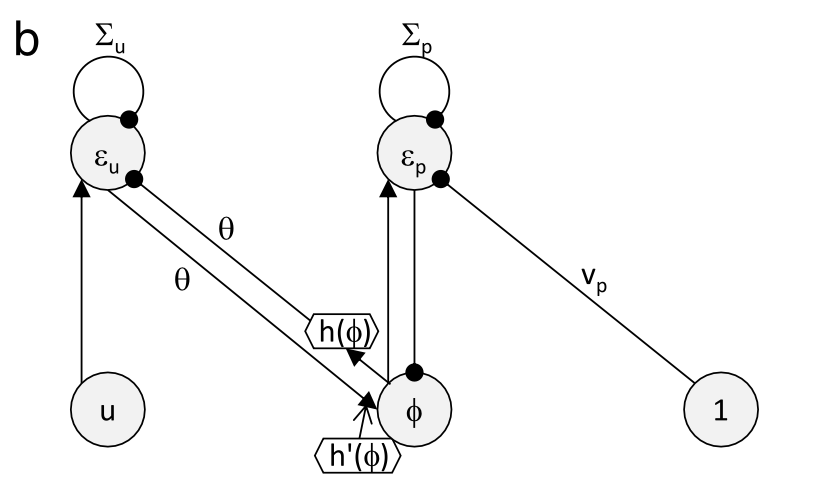
아까 말했던 F를 이제 Free Energy라고 부를 것인데요 이를 잘 살펴보면 q(v)가 v의 실제 분포라고 할때 DKL(q(v), p(v|u))를 최소화 하는 것과 Free Energy를 최대화 하는 것과 동치임을 알 수 있습니다. (q(v)에 phi에서의 delta function을 넣었을 경우) 이것이 Free-Energy의 개념입니다. 또 위 모델을 여러 변수에 의한 것으로 일반화 시키면 아래와 같이 나타낼 수 있습니다.

여기에 마지막으로 각각의 층에 대한 입력값이 이전 층의 출력값이 되게 hierarchy를 도입하고 error node를 통해 local plasticity 문제를 해결하면 신경과학적으로 설명이 되는 모델이 완성됩니다.

(설명이 논문만큼 자세하지 못했다는 부분은 양해 바랍니다. 논문을 읽는 것을 강력 추천합니다.)
실습은 Exercise 5에 대한 것만 약간 의아할 수 있으므로 이에 대한 파이썬 코드를 참고삼아 마지막에 첨부하였습니다.
마지막으로 이 논문을 읽으며 들었던 의문점 또는 질문에 대해 적고 마무리합니다. (아래 부분은 정리하지 않았습니다.)
1. 실제로 u 등의 값이 가지는 신경학적 의미가 무엇인지(firing rate 인지 stim인지) 왜냐하면 양의 값으로 범위가 제한이 되어 있지 않다.
2. 여기서는 gaussian을 두고 사용하였는데 실제 뇌도 gaussian 가정을 하고 문제를 푸는지, 즉 이것이 자연스러운 과정인지 또 gaussian이 아닌 분포에 대해서도 학습이 가능한지 아니면 실제 뇌는 gaussian 아닌 것은 어려움을 겪는지
3. 실제로 뇌에서 비슷한 connection이나 역할을 하는 부위가 발견된 논문이 존재하는지
=> Bastos et al. (2012), Friston, 2010; Friston et al., 2013
4. 이 정도 우연이라면 우연이 아니다. 실제라고 생각될 정도의 유력한 이론이다. 실제 신경에 관하여 어디 뇌 부위까지 적용이 가능한건가 인지기능에 대해서는 되는가
5. 임의의 KL divergence도 이와 비슷한 패러다임으로 신경학적 모델링이 가능한가? 그러면 머신러닝이 머리에서 구현된다는 의미로 보인다.
6. Predictive Coding과 ML이 섞이거나 이를 연관되어 서술한 논문은 어떻게 있는가
7. 이를 반도체로 만들 수 있는가
8. memory에 대해서는 사람들이 computational 하게 어떻게 생각하는가
9. feedback 등 여러 최적화에 hebbian 으로 다가가는 수학적 테크닉의 이해
10. 창작자 관점에서 어떤 사고로 이 연구를 할 수 있었는지 이해 초기 상황 이해